Kruskal's algorithm(크루스칼/크러스컬 알고리즘)
최소 비용 신장 트리를 찾는 알고리즘
모든 정점을 최소 비용으로 연결하는 최적의 해답을 구하는 것
시간복잡도
O(ElogV)
동작 과정
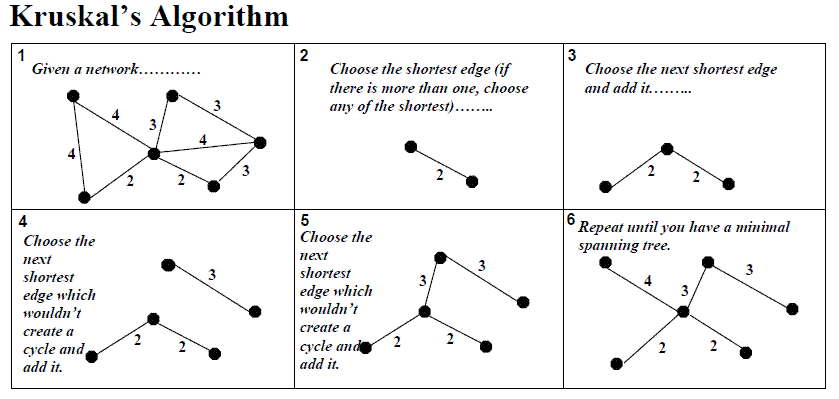
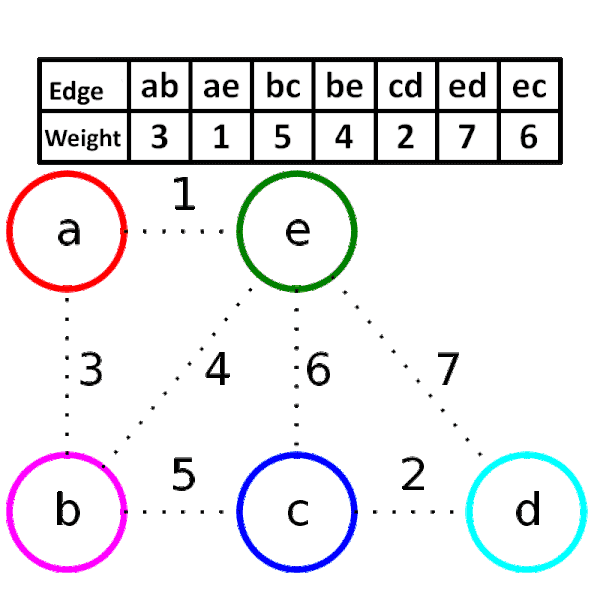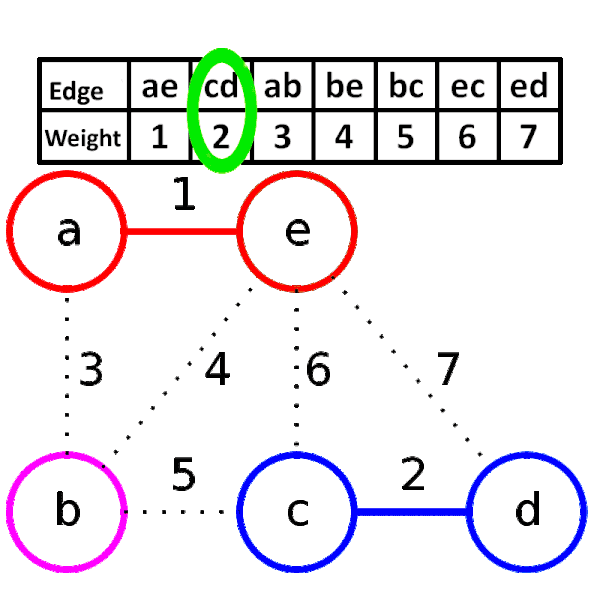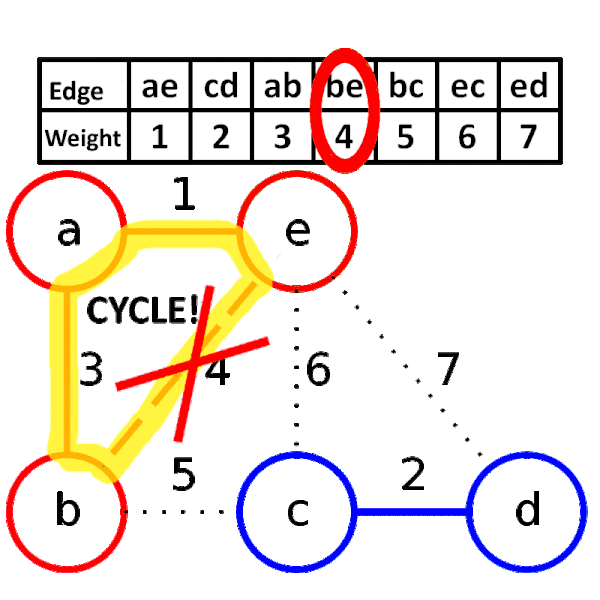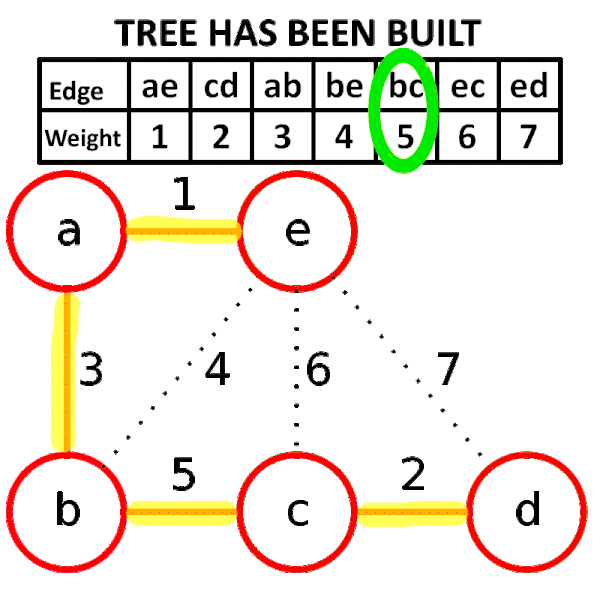
1. 그래프의 간선들을 가중치의 오름차순으로 정렬한다.
2. 가중치가 작은 간선부터 선택한다.
3. 사이클을 형성하는 간선은 제외하고, 사이클을 형성하지 않는 경우는 해당 간선을 집합에 추가한다.
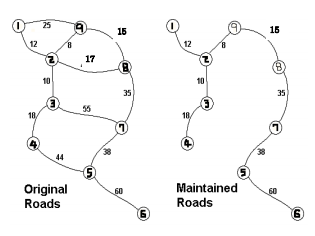
모든 도시를 연결하면서 드는 최소비용을 구하는 프로그램
import java.util.ArrayList;
import java.util.Collections;
import java.util.Scanner;
class Edge implements Comparable<Edge> { // 가중치 방향 그래프
int vertex1; // 시작 정점
int vertex2; // 이동 정점
int cost; // 가중치
Edge(int vertex1, int vertex2, int cost) {
this.vertex1 = vertex1;
this.vertex2 = vertex2;
this.cost = cost;
}
@Override
public int compareTo(Edge ob) {
return this.cost - ob.cost; // 가중치 기준 오름차순
}
}
public class Main { // Union&Find
static int[] parent;
static int answer = 0;
public static int find(int v) {
if (v==parent[v]) return v;
else return parent[v] = find(parent[v]); // 경로 압축 (Path Compression) // 재귀
}
public static void union(int a, int b) { // 합연산
int fa = find(a);
int fb = find(b);
if (fa!=fb) parent[fa] = fb;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int v = scanner.nextInt(); // 도시의 개수 // vertex
int e = scanner.nextInt(); // 도로의 개수 // edge
ArrayList<Edge> graph = new ArrayList<>();
parent = new int[v+1]; // 1~v까지 사용
for (int i=1; i<=v; i++) parent[i] = i; // 초기화
for (int i=0; i<e; i++) {
int a = scanner.nextInt(); // 도시
int b = scanner.nextInt(); // 도시
int c = scanner.nextInt(); // 도로 유지비용
graph.add(new Edge(a,b,c));
}
Collections.sort(graph); // 정렬
for (Edge temp : graph) {
if (find(temp.vertex1)!=find(temp.vertex2)) {
answer += temp.cost;
union(temp.vertex1, temp.vertex2);
}
}
System.out.println(answer);
}
}9 12
1 2 12
1 9 25
2 3 10
2 8 17
2 9 8
3 4 18
3 7 55
4 5 44
5 6 60
5 7 38
7 8 35
8 9 15
196
'알고리즘(Java) > Greedy Algorithm' 카테고리의 다른 글
| [알고리즘]원더랜드(최소 신장 트리 : Prim/Priority Queue) (0) | 2021.09.03 |
|---|---|
| [알고리즘]친구인가? (Disjoint-Set/Union&Find) (0) | 2021.09.02 |
| [알고리즘]Dijkstra(다익스트라) + Priority Queue (0) | 2021.09.02 |
| [알고리즘]최대 수입 스케쥴(PriorityQueue) (0) | 2021.09.02 |
| [알고리즘]회의실 배정 (0) | 2021.09.02 |




댓글