Dijkstra(다익스트라)
그래프에서 꼭짓점 간의 최단 경로를 찾는 알고리즘
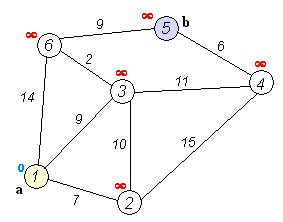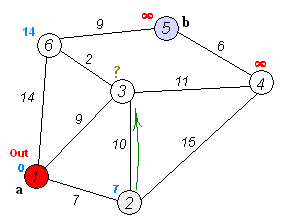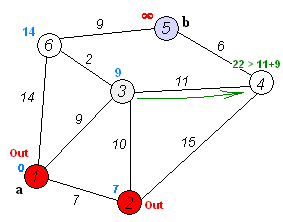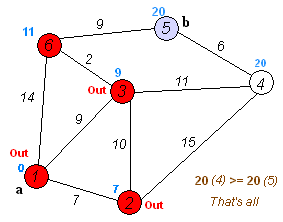
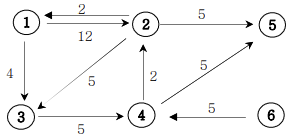
아래의 가중치 방향그래프에서 1번 정점에서 모든 정점으로의 최소 거리비용을 출력하는 프로그램
import java.util.ArrayList;
import java.util.Arrays;
import java.util.PriorityQueue;
import java.util.Scanner;
class Edge implements Comparable<Edge> {
int vertex; // 정점
int cost; // 가중치
Edge(int vertex, int cost) {
this.vertex = vertex;
this.cost = cost;
}
@Override
public int compareTo(Edge ob) {
return this.cost - ob.cost; // 가중치 기준 오름차순
}
}
public class Main { // O(n)
static int n, m;
static int[] dis;
static ArrayList<ArrayList<Edge>> graph;
public static void solution(int s) {
PriorityQueue<Edge> pQ = new PriorityQueue<>(); // 우선순위 큐 // 오름차순
pQ.offer(new Edge(s,0)); // 정점1, 가중치0
dis[s] = 0; // 1에서 1까지의 가중치 : 0
while(!pQ.isEmpty()) {
Edge temp = pQ.poll(); // cost 가장 작은 게 poll된다
int nowV = temp.vertex; // 현재 정점
int nowC = temp.cost; // 현재 가중치
if (nowC>dis[nowV]) continue;
for (Edge ob : graph.get(nowV)) {
if (nowC+ob.cost<dis[ob.vertex]) {
dis[ob.vertex] = nowC + ob.cost;
pQ.offer(new Edge(ob.vertex, nowC+ob.cost));
}
}
}
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt(); // 정점의 수
m = scanner.nextInt(); // 간선의 수
dis = new int[n+1]; // 최소비용 담을 배열 // 1~n까지 사용할 것
Arrays.fill(dis, Integer.MAX_VALUE); // 무한대로 초기화
graph = new ArrayList<ArrayList<Edge>>(); // 가중치 방향 그래프
for (int i=0; i<=n; i++) {
graph.add(new ArrayList<Edge>());
}
for (int i=0; i<m; i++) {
int a = scanner.nextInt(); // 기준 정점
int b = scanner.nextInt(); // 연결된 정점
int c = scanner.nextInt(); // 거리비용(가중치)
graph.get(a).add(new Edge(b,c));
}
solution(1); // 1번 정점부터 시작
for (int i=2; i<=n; i++) {
if (dis[i]!=Integer.MAX_VALUE) System.out.println(i + " : " + dis[i]);
else System.out.println(i + " : impossible");
}
}
}6 9
1 2 12
1 3 4
2 1 2
2 3 5
2 5 5
3 4 5
4 2 2
4 5 5
6 4 5
2 : 7
3 : 4
4 : 9
5 : 7
6 : impossible
'알고리즘(Java) > Greedy Algorithm' 카테고리의 다른 글
| [알고리즘]원더랜드(최소 신장 트리 : Kruskal/Union&Find) (0) | 2021.09.03 |
|---|---|
| [알고리즘]친구인가? (Disjoint-Set/Union&Find) (0) | 2021.09.02 |
| [알고리즘]최대 수입 스케쥴(PriorityQueue) (0) | 2021.09.02 |
| [알고리즘]회의실 배정 (0) | 2021.09.02 |
| [알고리즘]씨름선수 (0) | 2021.09.01 |



댓글